Proficient in Signal Processing Design Small Tips(8): Detecting signals submerged in noise

The author of this article, maxfiner, graduated from Xi'an University of Electronic Science and Technology with a master's degree in signal and information processing. Maxfiner has worked in the wireless communication department of Huawei Communication Technology Co., Ltd., and has many years of experience in engineering project development. It also has algorithm theory research, simulation verification, and corresponding hardware design implementation capabilities. It has practical experience in all aspects of communication physical layer development and design. .

The correlation function is widely used, such as the detection of signals in noise, the implicit detection of signals, the measurement of signal length and so on. This section is devoted to the use of autocorrelation functions to detect periodic signals that are submerged under noise.

A signal, due to the influence of noise, is completely unrecognizable from the waveform. As shown below:

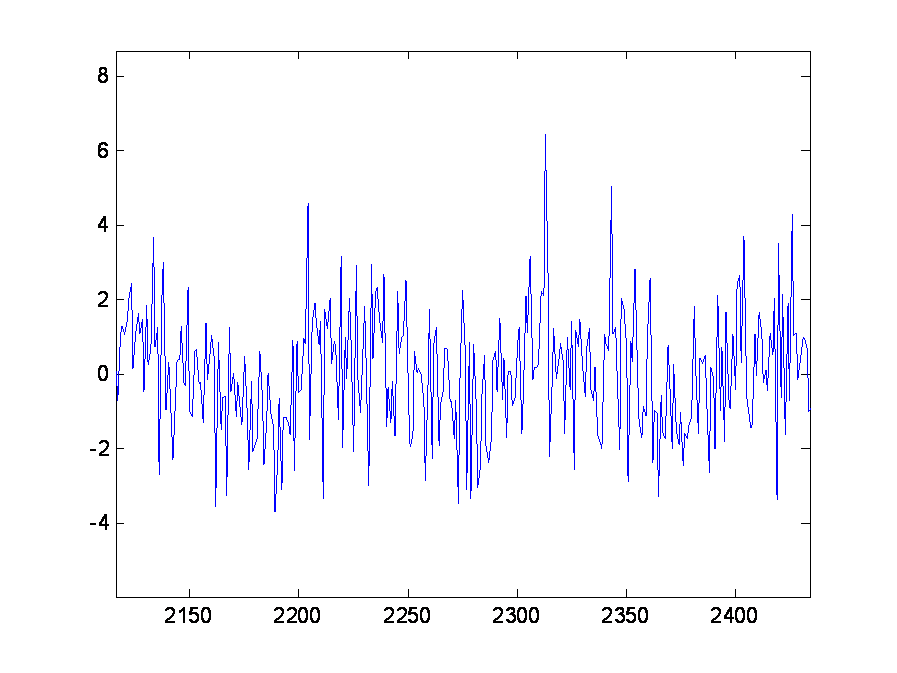
Signal-based autocorrelation accumulation can detect the presence of periodic signals, based on several preconditions:

First, noise is often treated as additive white noise because it is theoretically easy to analyze and process. The white noise autocorrelation function has a very unique personality, which is the autocorrelation function. 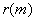Only in 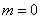There are certain values ​​when 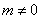Then it is zero. This is determined by the complete randomness of the white noise itself. It is also based on this property that we are able to extract the signals we are interested in from the background of strong noise.

Second, the autocorrelation function of the periodic signal is still a periodic function, and the period is the same as the original function period. This can be easily derived from the definition of the autocorrelation function.

Third, white noise and periodic signals are completely uncorrelated, and the complete randomness of white noise causes it to be unrelated to any function. The cross-correlation function between them can be considered to be zero. This is a prerequisite for many theoretical derivations.

Based on the definition of the autocorrelation function, we can make a simple derivation from the formula to see what the autocorrelation function of the signal after the noise is added. Suppose our signal is 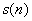, the white noise signal is 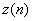, the signal with white noise added is .

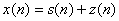Then, based on the above three premises, we can 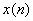Autocorrelation function 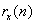Expressed as follows. Formula derivation seems to be very troublesome. In fact, there are strict rules and reasons step by step. Careful observation and analysis can enhance the understanding of autocorrelation function and cross-correlation function, and can also strengthen the basic ability of formula derivation.

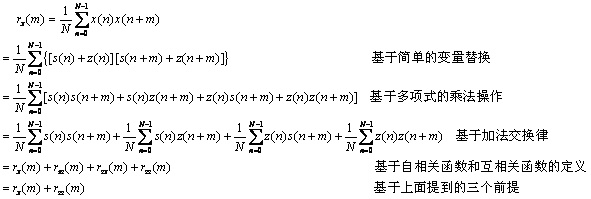
That is,

The theoretical formula is very rigorous but not intuitive. Still find a practical example to verify it. Construct a sine wave periodic signal and a white noise signal to see what the autocorrelation function of the superimposed signal looks like.

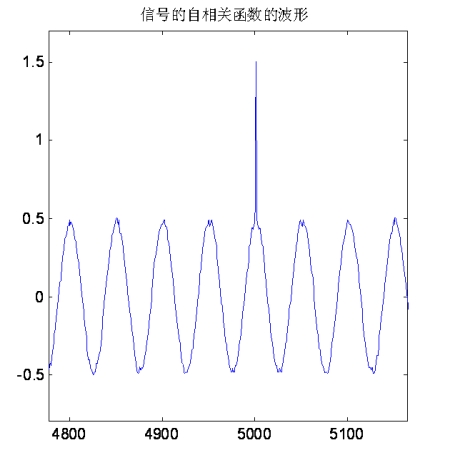
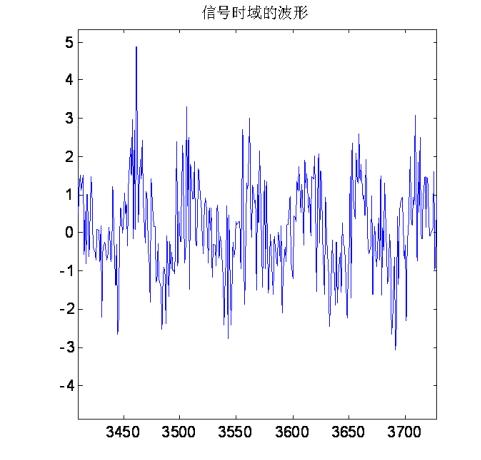
The autocorrelation function is a relatively large value at the 0 position, which is caused by the associated accumulation of white noise itself. In the non-zero position, it is completely determined by the periodic signal.

The corresponding matlab simulation verification code is as follows.

Fs = 5e3;

n = 0: 1 / fs: 1;

Len = length(n);

Freq = 100;

s = sin(2*pi*freq*n);

n = randn(1,len);

x = s + n;

Rr = xcorr(x, 'unbiased');

Figure,subplot(121),plot(x);TItle('ÐÅoÅʱÓòμÄ2 ̈ÐÎ');

Subplot(122),plot(rr);TItle('ÐÅoÅμÄ&TImes;ÔÏà1Øo ̄ÊýμÄ2 ̈ÐÎ');

It is worth noting that the correlation function uses the function xcorr provided by the matlab toolbox. It has two calculation methods, one is called “biased”, which is biased. One is called "unbiased", which is unbiased. This is because the actual data length is always limited when the correlation function is actually calculated. Then, as the m in the correlation function increases, the number of related cumulative sums is gradually reduced. When the above-mentioned autocorrelation is adopted. When the function calculates the formula, the uniformity is divided by N, which causes the correlation function to decrease linearly with the increase of m. This is the biased calculation method, which means that the statistical mean and actual value of the calculated value are inconsistent, and there is a certain Deviation. This calculation results in an error that becomes larger as the absolute value of m approaches the actual acquisition signal length N. If the factor of decreasing the cumulative sample caused by the increase of m is taken into consideration, instead of dividing N by N, but dividing by Nm, the correlation function will no longer produce a linear decrease problem, which corresponds to the unbiased in the code. Calculation.

The next issue begins - proficient in signal processing design small TIps (9): Estimate the delay of the signal in the analog channel, so stay tuned!

Disclaimer: Electronic enthusiast network copyright, declined to reprint!

Plastic Housing Coffee Grinder

Hand Coffee Grinder,Conical Burr Coffee Grinder,Home Coffee Grinder,Plastic Housing Coffee Grinder,blade coffee mill,Automatic burr mill

FOSHAN FORTUNE ELECTRICAL APPLIANCE CO.,LTD , https://www.coffelady.com