All kinds of electrical equipment on modern airplanes are increasing day by day, and the power consumption is increasing, which puts strict requirements on the capacity, power supply quality and reliability of airborne power supplies. With the continuous application of advanced technology on aircraft, the reliability of aircraft power supply system is becoming higher and higher. Aircraft power distribution system is an important part of power supply system, so it is of great significance to study the reliability of power distribution system. The existing reliability analysis methods include minimum path method, minimum cut set method, fault tree analysis method, and failure mode consequence analysis method. Although these reliability analysis methods can calculate the reliability index of the power distribution system more effectively, in practical applications, the calculation amount is very large during the qualitative analysis of large and complex systems, and even NP difficult problems may be formed.
Petri is a mathematical and graphical analysis tool for system description and simulation, which can express the static structure and dynamic changes of the system. Therefore, this paper proposes a reliability analysis method of aircraft power distribution system based on Petri net.
1 Petri net overview
As a kind of special directed network, Petri net takes the place and transition as nodes, and the directed direction of directed arc expresses the propagation relationship of system faults. The state of the system is represented by a place, and the event that changes the state is represented by a transition (transacTIon). In the graphical description of Petri nets, "○" is used to represent the place, "|" is used to represent the transition, and the directed arc "→" is used to indicate the sequence couple, and thus constitute the graphical representation of the Petri net. If the weight of all directed arcs of a Petri net is 1, then this net is called the canonical net. Only the situation of the regulatory network is considered here.
The six-tuple N = (P, T, I, O, M, Mo) is called a Petri net if the following conditions are met.
1) P = {P1, P2 ..., Pn} is a limited set of places, n is the number of places, n> 0;
2) T = {T1, T2 ..., Tm} is a finite set of transitions, m is the number of transitions, m> 0, P∩T = empty set;
3) I: PxT → N is the input function, which defines the set of directed arc repetition numbers or weights from P to T, where N = {0, 1 ...} is a non-negative integer set;
4) I: TxP → N is the input function, which defines the set of directed arc repetition numbers or weights from T to P;
5) M: P → N is the distribution of signs in each store;
6) MO: P → N is the initial logo distribution in each store.
The application of Petri net to analyze the system failure is to take the undesirable event of the system as the top place, and to find out all possible factors leading to this event as the middle place and the bottom place. The basic elements of Petri nets-the different connections between the place and the transition can represent the logical relationship of the fault tree model, and the method of graph theory can be fully used to solve the diagnosis and reasoning problem of the fault model. The top event, middle event, and bottom event in the fault tree are represented by the place, transition, and arc in the Petri net, as shown in Figure 1.
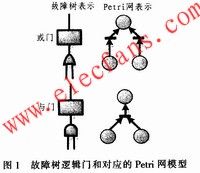
2 Reliability analysis based on Petri net
2.1 Qualitative analysis
The Petri net model simplifies the various logical connection relationships of the fault tree to only consist of the place and the transition. The network with the directed arc as the connection edge makes the fault model of the system simple and easy to understand, and the propagation relationship of the fault is clear. At present, many scholars have put forward many methods of using Petri net to find the minimum cut set, such as path search method and location matrix method. This paper mainly introduces a new algorithm that uses Petri net's correlation matrix to find the minimum cut set. This algorithm directly derives the cut set from the correlation matrix according to the input and output relationships expressed in the specified correlation matrix. It is easy for computer programs to implement, and for It is simpler and more intuitive to find the cut set of the Petri net model with repeated events.
The structure of the Petri net can be represented by a matrix. If the input function from the place P to t is a non-negative integer w, denoted as I (P, t) = w, then use a directed arc from P to t with a marginal w to indicate; if the place The output function from t to P takes the value of a non-negative integer w, denoted as O (P, t) = w, then it is represented by a directed arc from t to P with a marginal w. In particular, if w = 1, there is no need to mark; if I (P, t) = 0 or O (P, t) = 0, there is no need to draw an arc. Both I and O can be expressed as nxm non-negative integer matrix, the difference between O and I A = OI is called the correlation matrix. For canonical networks, w = 1. An example is given below to introduce the method steps of the minimum cut set of the association matrix.
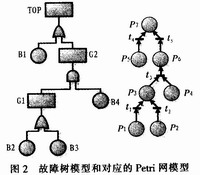
Find the correlation matrix from the Petri net model in Figure 2:

It can be seen that in this correlation matrix, -1 indicates that the directed arc is directed to the transition by the location, and this location is the input location of the transition; 1 indicates that the directed arc is directed by the transition to the location, and this location is the output of the transition. Treasury. The steps to find the minimum cut set of Petri net according to the above correlation matrix are as follows:
1) Find the rows with only 1 and 0, and no -1 in the correlation matrix, then this row corresponds to the top place (only the input place, no output place), so the place begins to look for (in this correlation matrix Is the last line).
2) Starting from 1 of the row corresponding to the top library, find -1 by column. The row represented by the row corresponding to -1 is an input library of the top library. If there are multiple -1s in the column, the corresponding There are multiple input locations for the same transition, and the input locations are in "phase and" relationship.
3) The -l found by step 2) searches for 1 by line, if there is 1 indicating that the place is an intermediate place, then it will search according to step 2) until the line does not have 1; if there is no 1, it means the library The place is a bottom place; if there are multiple 1s in the row, it means that the place corresponding to these 1s should be in a "phase or" relationship.
4) Continue searching according to step 2) and step 3) until the bottom place is found.
5) According to the previous "phase and" and "phase or" relationship, expand the base library to get all cut sets.
6) Obtain the minimum cut set according to the Boolean absorption law or the prime number method.
Follow the steps above to write:
P7 = P6 + P5 = P3xP4 + P5 = (P1 + P2) × P4 + P5 = P1 × P4 + P2 × P4 + P5
It can be seen that the minimum cut set is {P1, P4}, {P2, P4}, {P5}.
2.2 Quantitative calculation
After all the minimum cut sets of the fault tree are obtained, the probability of occurrence of the top event can be obtained by the minimum cut sets. Let the probability of occurrence of the top event be P (T), C1 = {P1, P4}, C2 = {P2, P4}, C3 = {P5}. then:
3 Reliability analysis of aircraft power distribution system based on Petri net
Figure 3 is a partial schematic diagram of a simplified distributed distributed power distribution system of an aircraft. It uses the non-channel automatic relay protection technology of the distribution line to control the opening and closing of circuit breakers and ring network switches to achieve the purpose of fault isolation and fault-tolerant power supply.
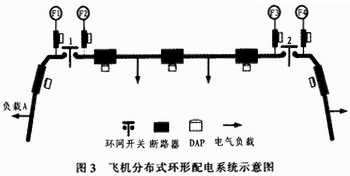
3.1 Establish fault tree
Figure 4 is a diagram of the fault tree model. In the figure, Fn represents the failure of generator n, and Kn represents the failure of ring switch of n.
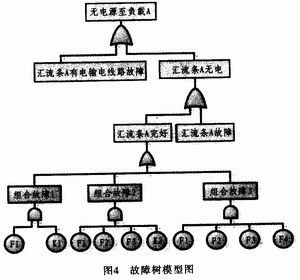
3.2 Transform fault tree model into Petri net model
Figure 5 is a Petri net model diagram, Pn represents the corresponding events in the fault tree of Figure 4 respectively.
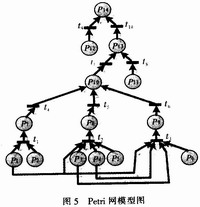
3.3 Using Petri Net's Association Matrix to Find the Minimal Cut Set
According to the above steps to find the minimum cut set:
P14 = P13 + P12 = P10 + P11 + P12 = P7 + P8 + P9 + P11 + P12 = P1P2 + P1P3P4P5 + P1P3P4P6 +
P11 + P12
Thus the minimum cut set is obtained: C1 = {P1, P2}, C2 = {P1, P3, P4, P5}, C3 = {P1, P3, P4, P6}, C4 = {P12} C5 = {P12}. Similarly, the probability of occurrence of the top event can be obtained by using the above quantitative calculation method.
4 Conclusion
The fault tree analysis method is often used in the reliability analysis of aircraft power distribution systems. Although the reliability analysis of the power distribution system is well solved, the practical application shows the disadvantages of complicated analysis and large amount of calculation, which is not conducive to power distribution. The system performs quick and effective evaluation. Converting the fault tree model to a Petri net model for analysis and calculation can greatly simplify the calculation in fault tree analysis and make up for the shortcomings of traditional fault tree analysis methods.
Shenzhen Priva Tech Co., Ltd. , https://www.privaled.com
