In February of this year, a group of UC Berkeley and Stanford posted an article in arXiv:
SqueezeNet: AlexNet-level accuracy with 50x fewer parameters and <0.5MB model size(https://arxiv.org/abs/1602.07360)
This article has made what many people dream of - compressing neural network parameters. But unlike the past, the original is not based on the predecessor network (such as Deep Compression), but designed a new network, it uses 50 times less parameters than AlexNet, to achieve the same accuracy of AlexNet!
Regarding SqueezeNet's innovations and network structure, several fans in China have released relevant profiles, such as this (http://blog.csdn.net/xbinworld/article/details/50897870), this (http:/ /blog.csdn.net/shenxiaolu1984/article/details/51444525), foreign literature has not been checked, I believe there are certainly many.
The focus of this article is on why SqueezeNet can achieve network slimming? Is the redundancy of network parameters so strong? Or is it that many parameters are wasteful and meaningless?
In order to better explain the above problems, first give the AlexNet and SqueezeNet structure diagram:
AlexNet
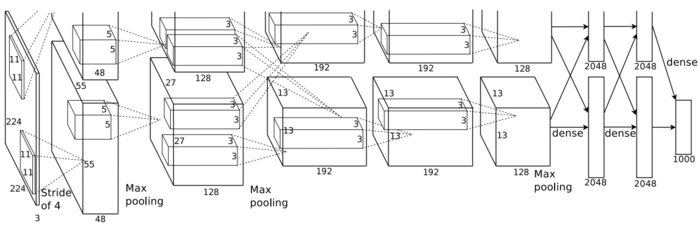
Figure 1 AlexNet schematic

Figure 2 AlexNet network structure
SqueezeNet
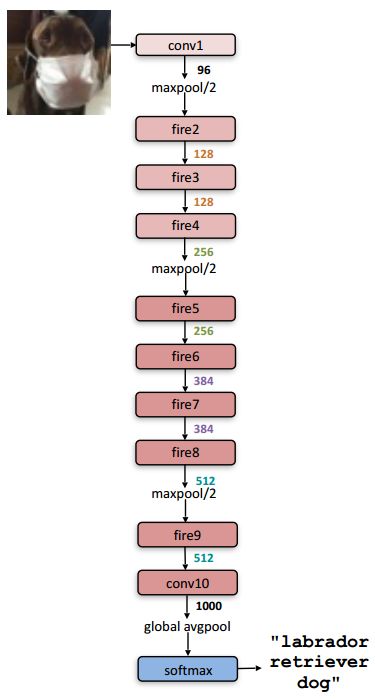
Figure 3 Schematic diagram of SqueezeNet

Figure 4 SqueezeNet network structure
Why does SqueezeNet achieve the same accuracy with AlexNet with fewer parameters?
The table below shows the amount of parameters for SqueezeNet, which is only 1/48 of AlexNet.
| AlexNet | 60M |
| SqueezeNet | 1.25M |
At first glance, it feels very unscientific. How can the difference in the amount of parameters that achieve such disparity achieve the same recognition accuracy?
Let's consider a very simple example. This example can be said to be the epitome of SqueezeNet and AlexNet:
1, a layer of convolution, the size of the convolution kernel is 5 × 5
2, two-layer convolution, the size of the convolution kernel is 3 × 3
The above two convolution methods have the same size except for the convolution kernel. For the convenience of calculation, define the number of input channels, the number of output channels is C (two-layer convolution is C'), and the output size is N×N. .
According to current theories, neural networks should use multiple layers of small convolutions as much as possible to reduce the amount of parameters and increase the nonlinearity of the network. But as the parameters decrease, the amount of calculation increases! According to the above example, roughly calculate, for the sake of simplicity, only consider the calculation of multiplication:
The 5×5 layer convolution calculation is 25×C×N×N
The calculation amount of the 3×3 two-layer convolution is 9×C×(1+C')×N×N
It is obvious that 25C<9C(1+C').
This shows what? It shows that the "multi-layer small convolution kernel" does increase the amount of calculation!
Let's go back and consider SqueezeNet and AlexNet. The architecture of the two networks is as shown in the above four figures. It can be seen that SqueezeNet is much deeper than AlexNet, and SqueezeNet's convolution kernel is also smaller, which leads to the calculation of SqueezeNet. Far more than AlexNet (to be discussed, need to be further confirmed, because the squeeze layer in the Fire module has reduced the amount of calculation to some extent, SqueezeNet may not calculate much).
However, the original text of the paper pays too much attention to the number of parameters, ignoring the amount of calculation, such a contrasting approach does not seem appropriate. In fact, the latest deep neural network is to increase the amount of calculation in exchange for fewer parameters, but why is this good?
Because the memory reading takes much longer than the calculation time!
In this way, the problem is simple. Regardless of the advantages and disadvantages of the architecture of the network itself, the reason why the deep network is so successful is because the cost of parameter reading is transferred to the calculation amount, considering the current development level of human computers. The computational time is still much less than the data access time, which is also the root of the success of the "multiple small convolution kernel" strategy.
About Dense-Sparse-Dense (DSD) Training
I have to say this little discovery of the original, using the model after cropping as the initial value, and training again to adjust all the parameters, the correct rate can be increased by 4.3%. Sparse is equivalent to a regularization, and there is an opportunity to liberate the solution from the local minimum. This method is called DSD (Dense→Sparse→Dense).
How similar is this process to our human learning of knowledge! Humans revisiting the knowledge they have learned at regular intervals will increase their impression of what they have learned. We can interpret “interval†as “cuttingâ€, that is, forgetting those parameters that are not so important. “Re-learning†is understood as a new training, that is, strengthening the previous parameters to make it more accurate!
Led Floor Panels,Led Dance Floor Panel,48W Led Light Panel,Floor White Uplight Panel Led
Kindwin Technology (H.K.) Limited , https://www.ktlleds.com
