There are three main categories of artificial intelligence machine learning: 1) classification; 2) regression; 3) clustering. Today we will focus on the CART algorithm.
We know that the decision tree algorithm occupies two positions in the top ten machine learning, namely the C4.5 algorithm and the CART algorithm, which shows the importance of the CART algorithm. The following focuses on the CART algorithm.
Different from ID3 and C4.5, CART is a binary decision tree, which is a full binary tree. The CART algorithm was proposed by Breiman et al. in 1984. It uses a completely different method to construct prediction criteria from traditional statistics. It is given in the form of a binary tree, which is easy to understand, use and explain. The prediction tree constructed by the CART model is in many cases more accurate than the algebraic prediction criteria constructed by commonly used statistical methods, and the more complex the data and the more variables, the more significant the superiority of the algorithm.
The CART algorithm can be used for both classification and regression. The CART algorithm is called a landmark algorithm in the field of data mining.
CART algorithm concept:CART (Classification and Regression Tree) Classification and Regression Tree is a decision tree construction algorithm. CART is a learning method to output the conditional probability distribution of random variable Y under the condition of a given input random variable X. CART assumes that the decision tree is a binary tree, and the values ​​of the internal node features are "yes" and "no", the left branch is the branch with the value "yes", and the right branch is the branch with the value "no". Such a decision tree is equivalent to recursively dicing each feature, dividing the input space, that is, the feature space into a finite number of units, and determining the predicted probability distribution on these units, that is, the conditional probability of output under the given conditions of the input distributed.
The CART algorithm can handle both discrete and continuous problems. When this algorithm deals with continuous problems, it mainly uses binary segmentation to deal with continuous variables, that is, if the eigenvalue is greater than a given value, go to the left subtree or go to the right subtree.
CART algorithm composition:The CART algorithm is composed as follows:
1) Decision tree generation: Generate a decision tree based on the training data set, and the generated decision tree should be as large as possible; build nodes from the root from top to bottom, and choose the best one at each node (different algorithms use different indicators to define "Best") attribute to split the training data set in the child nodes as pure as possible.
2) Decision tree pruning: Pruning the generated tree with the verification data set and selecting the optimal subtree. At this time, the minimum loss function is used as the criterion for pruning. CCP (Cost-Complexity Pruning) is used here.
The generation of the decision tree is the process of recursively constructing a binary decision tree, using the square error minimization criterion for the regression tree and the Gini index minimization criterion for the classification tree to perform feature selection and generate the binary tree.
1) Regression tree generation
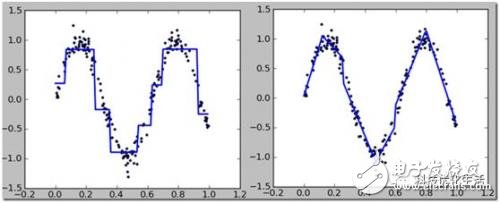
The regression tree uses the mean square error as the loss function. When the tree is generated, the space is recursively divided according to the optimal feature and the optimal value under the optimal feature until the stopping condition is met. The stopping condition can be set manually, such as when The loss reduction value after segmentation is less than the given threshold ε, then the segmentation is stopped and leaf nodes are generated. For the generated regression tree, the category of each leaf node is the mean value of the label falling on the leaf node data.
The regression tree is a binary tree, each time it is divided according to a certain value under the feature, each internal node is a judgment of the corresponding feature, until the leaf node gets its category, the difficulty of constructing this tree It lies in how to select the optimal segmentation feature and the segmentation variable corresponding to the segmentation feature.
Regression trees and model trees can handle both continuous and discrete features.
The regression tree generation algorithm is as follows:
Input: training data set D = {(x1, y1), (x2, y2),..., (xN, yN)}
Output: regression tree T
1) Solve the selected segmentation feature j and the segmentation feature value s, j divides the training set D into two parts, R1 and R2, after segmentation according to (j, s) as follows:
R1(j,s)={xi|xji≤s} R2(j,s)={xi|xji>s}
c1=1N1∑xi∈R1yi c2=1N2∑xi∈R2yi
2) Traverse all possible solutions (j, s) to find the optimal (j*, s*), the optimal solution minimizes the corresponding loss, and it can be divided according to the optimal feature (j*, s*) .
Min {∑ (yi–c1)ï¼¾2 +∑ (yi–c2)ï¼¾2ï½
j,s xi∈R1 xi∈R2
3) Recursively call 1) and 2) until the stop condition is met.
4) Return to the decision tree T.
The regression tree mainly adopts a divide-and-conquer strategy to divide and conquer targets that cannot be optimized by the only global linear regression, and then obtain more accurate results, but it is not a wise choice to take the mean by segment. You can consider setting the leaf node to A linear function, this is the so-called piecewise linear model tree. Experiments show that the effect of the model tree is better than that of the regression tree. The model tree only needs to be slightly modified on the basis of the regression tree. For the data allocated to the leaf nodes, the least mean square loss of linear regression is used to calculate the loss of the node.
2) Classification tree generation
The classification tree is used for classification in CART. Unlike ID3 and C4.5, the CART classification tree uses Gini index to select the optimal segmentation feature, and each time it is divided into two.
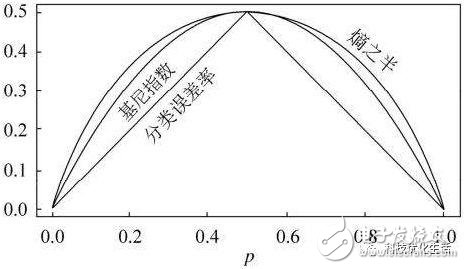
The Gini index is a concept similar to entropy. For a random variable X with K states corresponding to probabilities p1, p2,..., pK, the Gini index Gini is defined as follows:
Gini(X)=∑pk(1?pk)=1? ∑kp2k
kk
The Gini index of set D under the condition of known characteristic A:
Gini(D,A)=(|D1|/|D|)*Gini(D1)+(|D2|/|D|)*Gini(D2)
The larger the value of Gini (D, A), the greater the uncertainty of the sample, which is similar to entropy, so the criterion for selecting feature A is that the smaller the value of Gini (D, A), the better.
We usually use AVSS, AVS, TXL or cable with generally 18AWG or custom gauge to 16AWG or 14AWG.The connector we recommand is Tyco/AMP/Delphi/Bosch/Deutsch/Yazaki/Sumitomo /Molex replacements or originalTo be applied in automobile or motorcycle HID headlight upgrading system.
We can do any extension cable on GPS Tracking Systems & Driving recorder camera. If you need further question, our profeessional engineers are able to solve for you.
Camera Harness,Camera Wire Harness,Electrical Cable Crimper,Wiring Harness Clips
Dongguan YAC Electric Co,. LTD. , https://www.yacentercn.com
